《莱因德纸草书》(Rhind Papyrus)是公元前1650年左右的埃及数学著作，属于世界上最古老的数学著作之一，作者是书记官阿默斯。内容似乎是依据了更早年代（1849 B.C.—1801 B.C.)的教科书，是为当时的包括贵族、祭司等知识阶层所作，最早发现于埃及底比斯的废墟中。公元1858年由英国的埃及学者莱因德(A.H.Rhind)购得，故名《莱因德纸草书》，现藏于伦敦大英博物馆。该纸草书全长544 cm，宽33 cm。
纸草书的卷首栽录了一组分数分解表，把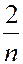
（n为5到101之间的奇数）分解为单位分数（分子为1的分数)之和。接着列出了87个问题，每个问题都给出了解答。问题3是10个人分6个面包，问各得多少。7～20题是分数的乘法运算。21～23题分别是将一已知分数变为单位分数之和。问题24～38的内容在今天可归为一元一次方程，其解法使用了假位法。其中后半部分(35～38题）是关于量器海克特（hekat）的使用问题，39～40题是关于面包分配的问题，涉及等差数列。如第40题为：把100个面包分给5个人，使每人所得成等差数列，且使最大的三份之和的
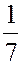是最小的两份之和，问各得多少。问题41～46是体积问题。48～55题为面积问题，其中有圆、正方形、等腰三角形、等腰梯形等。圆的面积是直径的九分之八的平方，即相当于取圆周率π＝3.16049。56～60题是金字塔问题，从中可看到三角学的初步知识。问题61以后是杂题，涉及许多实际问题，其中69～78题是关于食物中所含原料的比例问题，79题是一个等比数列问题，84题是牲畜饲料的分配问题，其他问题不甚完整。
《莱因德纸草书》是了解埃及数学的最主要依据，它准确地反映了当时埃及的数学知识的状况，鲜明地体现了埃及数学的实用性。它对我们应该如何看待数学的起源问题也有很大的启发。
